Benford’s Law

Benford’s Law

A fun fact for you today.  Did you know that in naturally occurring collections of numbers, the first significant digit is likely to be small?

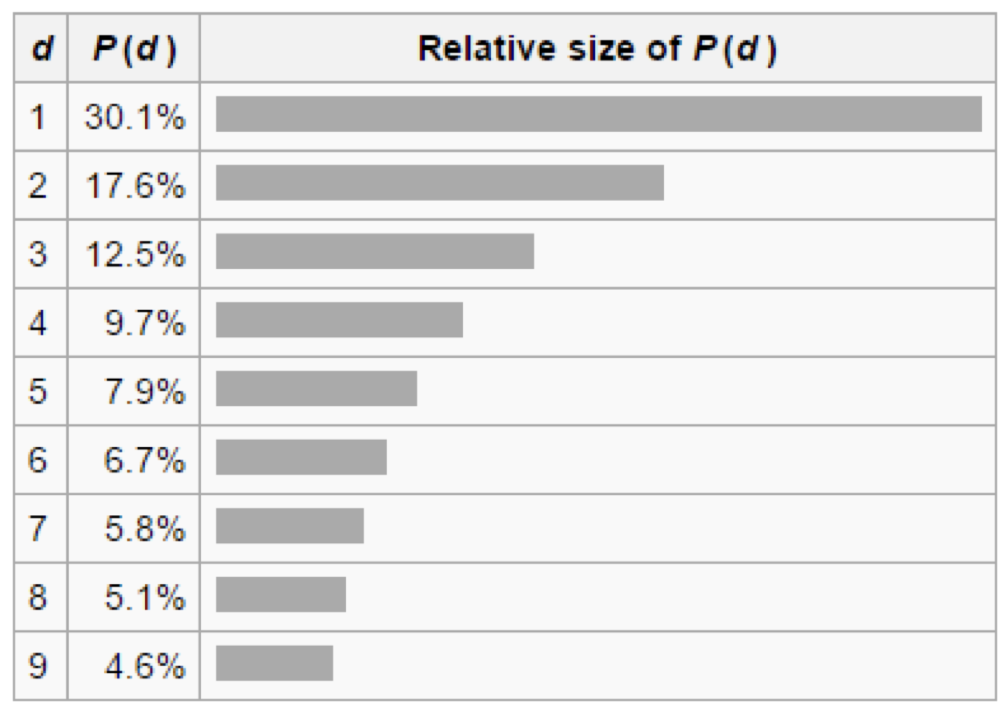
In fact, in many sets of numbers the first digit tends to be “1” about 30 per cent of the time, while “9” appears as the most significant digit only about 5 per cent of the time.  If the digits were distributed randomly, you would expect each to appear as the first significant digit 11.1 per cent of the time.

The chart below sets out the full probability distribution for sets that satisfy the so-called Benford’s Law.

I don’t know of an easy way to get your head around why this phenomenon arises, but it occurs where the logarithm of the data is evenly distributed, which tends to be the case for sets of numbers that span many orders of magnitude.

As to practical implications, one use for Benford’s Law is the detection of accounting fraud (as well as other types of numerical fraud).  Accounting data typically follows a Benford Law distribution, while made up numbers tend to be more uniformly distributed. If an analysis of a set of accounting numbers doesn’t show something like the distribution above, it might be time to ask questions.

Tim Kelley is Montgomery’s Head of Research and the Portfolio Manager of The Montgomery Fund. To invest with Montgomery domestically and globally, find out more.

MORE BY TimINVEST WITH MONTGOMERY

Tim joined Montgomery in July 2012 and is a senior member of the investment team. Prior to this, Tim was an Executive Director in the corporate advisory division of Gresham Partners, where he worked for 17 years. Tim focuses on quant investing and market-neutral strategies.

This post was contributed by a representative of Montgomery Investment Management Pty Limited (AFSL No. 354564). The principal purpose of this post is to provide factual information and not provide financial product advice. Additionally, the information provided is not intended to provide any recommendation or opinion about any financial product. Any commentary and statements of opinion however may contain general advice only that is prepared without taking into account your personal objectives, financial circumstances or needs. Because of this, before acting on any of the information provided, you should always consider its appropriateness in light of your personal objectives, financial circumstances and needs and should consider seeking independent advice from a financial advisor if necessary before making any decisions. This post specifically excludes personal advice.