
A distribution of valuations
Having finished an advanced mathematics degree, one question my peers often ask me is how does maths fit into investing? Today I wanted to focus on one of the ways maths can help shape investing decisions – in particular: probability distributions.
You may recall learning about the normal distribution at school… it looked something like this:
Distributions can be very helpful in looking at big pools of known data – such as average test results, or stock returns. The normal distribution will help you predict how likely an outcome is if you know the average return of the data and the standard deviation.
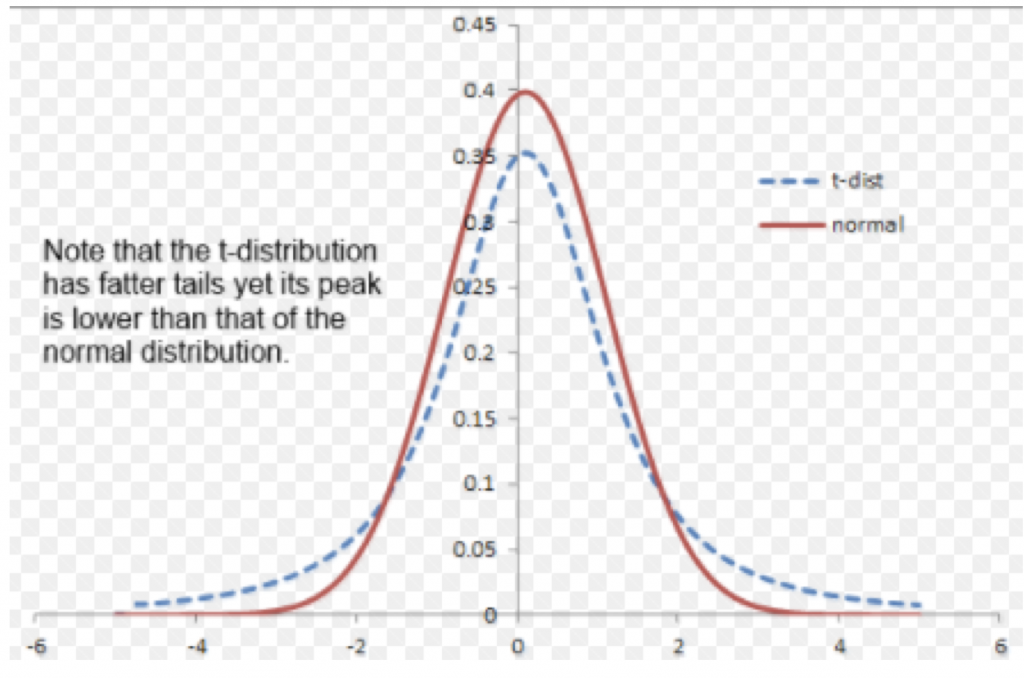
Now different distributions can have different properties – the t-distribution shows fatter tails. This means that non-average outcomes are more likely:
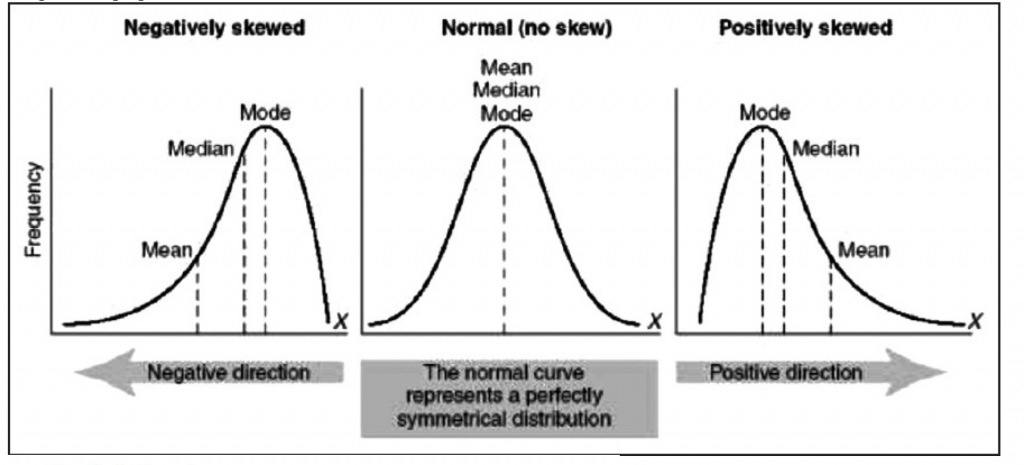
Other distributions may have a skew – where the modal – or most common outcome – isn’t the same as the average. These distributions will have one tail fatter.
So how does this come into investing?
When forecasting future cashflows it would be foolish to assume one can achieve 100 per cent accuracy. It is therefore important to recognise that each forecast is not a precise number but a representation of a distribution of outcomes. This is why it can be very helpful to form base, bull and bear cases and also run sensitivity tests. These scenarios can help you get a sense of what the distribution looks like and help you make effective investment decisions.
Two examples of how this can affect investments are:
- Returns in a company with contract risk will be trading on a distribution with fatter tails than one with lots of recurring revenue. Less solutions will land precisely on the average.
- A stock which has 10 per cent upside from the base case but a big negative skew (for example a company may have a large contract up for renewal), may not offer as good a risk-reward as one trading 10 per cent below valuation in a normal distribution.
Investing isn’t black and white, it’s what makes it wonderfully challenging and removes the possibility of certain returns. However – you can consistently maximise your probability of success.
This post was contributed by a representative of Montgomery Investment Management Pty Limited (AFSL No. 354564). The principal purpose of this post is to provide factual information and not provide financial product advice. Additionally, the information provided is not intended to provide any recommendation or opinion about any financial product. Any commentary and statements of opinion however may contain general advice only that is prepared without taking into account your personal objectives, financial circumstances or needs. Because of this, before acting on any of the information provided, you should always consider its appropriateness in light of your personal objectives, financial circumstances and needs and should consider seeking independent advice from a financial advisor if necessary before making any decisions. This post specifically excludes personal advice.
INVEST WITH MONTGOMERY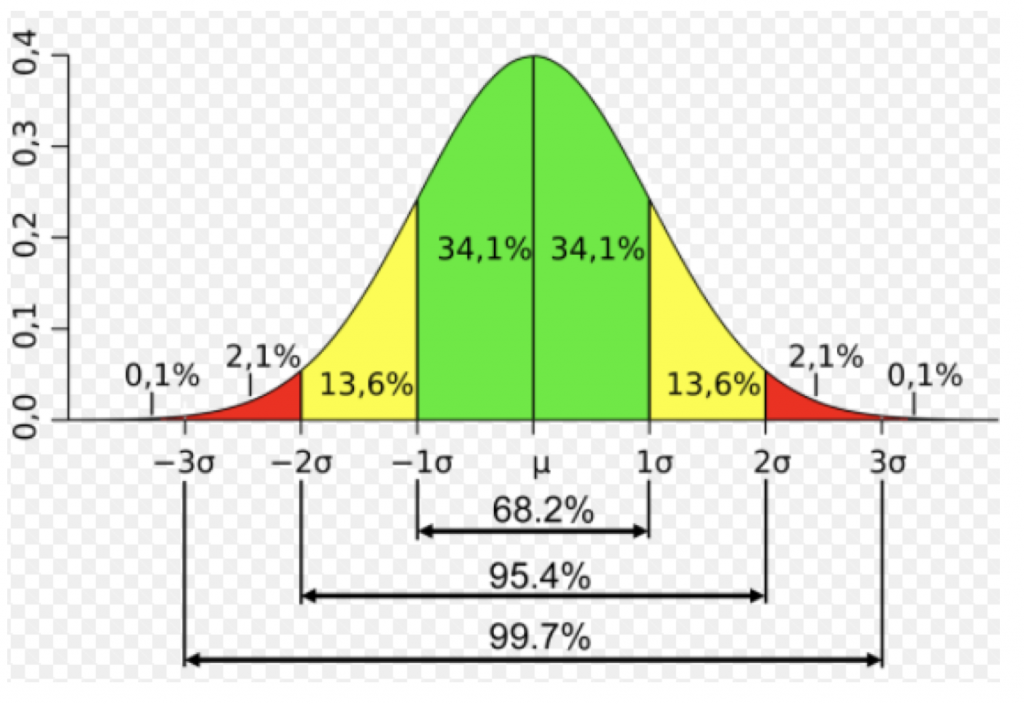
Hi Lisa, I would love to hear your view on the economic system we live with and it’s apparent weaknesses which seem to be mainly that the entire system relies on theory’s and not mathematical based systems such as blockchain .As the theory’s themselves obviously run with large fat tail risks which have resulted in a very destructive boom bust bubble driven system requiring an ever increasing and unsustainable amount of debt and stimulus to barely maintain itself. It seem obvious that current economic theories need a substantial dose of mathematical enhancement .I realise it may be to big an ask to answer on here and even just a general opinion from a mathematician would be very interesting to me, Thankyou and regards, Andrew.
Andrew – I’ll leave you with a couple of thoughts and an anecdote.
In physics I studied something called chaos (aptly named). A chaotic system is one which is extremely sensitive to initial conditions and can lead to radically different outcomes from tiny differences (think of the butterfly effect). Two great examples of such systems are weather and the stock market. What this means is it is extremely difficult to predict prices and they can be sensitive to minuscule changes in the economy.
Modern economic theories rely heavily on making simplifying assumptions to explain the system – the market efficiency hypothesis stands out here. Creating assumptions to better explain a system is done plenty of times in maths and physics too (eg. the mathematics behind the Big Bang theory assumes homogeneity and isotropy (think uniformity) of space).
Whilst I’ve always been taught to never say never – it is common practice to explain elements of chaotic systems by creating some simplifying assumptions. Whilst this won’t be a perfect picture – it’ll certainly help explain the chaos.
And now for the anecdote:
A mathematician, a statistician, an engineer were each required to bet a wager on a horse race following their dissertation. The engineer bet confidently knowing that he had measured all the horses and calculated their strength and mechanical advantage to figure out their speed.
The statistician rolled his eyes and said he’s mistaken the regression. The engineers model failed to take individual variations into account. Instead he evaluated all previous performances of the horses under different conditions so bet on the best probability horse.
The mathematician laughed off their techniques and explained why he would win. “Well,” he says, “first I assumed all the horses were identical and spherical…”
Thanks Lisa, I guess chaos shall reign for now, it’s just the parabolic nature of debt and money creation that seems to contradict Long term sustainability and grantee ever increasing chaos which does not seem ideal. Thankyou and merry xmas.
Anytime – merry Christmas to you too!
Many thanks Lisa. Appreciate your help and may you enjoy a super Christmas period.
Thanks Lester, you too!
Great article Lias. I too love the challenge and opportunities that maths brings to investing. Could you possibly recommend some appropriate reading or short courses on the subject ? I have a degree in engineering so maths is a keen contest and not a hardship.
Great question – for an investing focussed read on this idea I would recommend Expectations investing by Michael Maboussin – it’s a fantastic book and a quick read.
For more mathematical focussed read I personally find courses better than books (gives you more of a chance to practice). Subjects in econometrics and financial mathematics cover this. You can also find a lot of online resources and youtube channels that offer introductions to probability distributions eg: jbstatistics: https://www.youtube.com/channel/UCiHi6xXLzi9FMr9B0zgoHqA also the Khan academy, they arrange their videos by subject: https://www.youtube.com/user/khanacademy/playlists
Hope that helps!